Matriks- Operasi Matriks, Penjumlahan, Pengurangan, dan Perkalian

Operasi Matriks 

Operasi yang berlaku pada matriks hanya penjumlahan, pengurangan dan perkalian.
Baca juga Ringkasan Matriks- Pengertian, Jenis, Ordo, Transpose

Penjumlahan dan Pengurangan Matriks

Penjumlahan dan pengurangan elemen-elemen yang bersesuaian pada matriks. Syarat penjumlahan dan pengurangan pada matriks harus mempunyai ordo sama. 

Sifat-sifat yang berlaku pada penjumlahan dan pengurangan matriks ;

1. Komutatif ( Ditukar)

    A + B = B + A

2. Asosiatif ( Dikelompokkan)

    ( A + B )+ C = A + ( B+ C)

3. Matriks nol adalah identitas penjumlahan

4. A + (-A ) = O

    "-A" adalah lawan dari A

5. A - B tidak sama B - A

Contoh 1 :

Misalkan diberikan matriks A berordo 2x2 dan B berordo 2x2 sebagai berikut:

$A=\left(\begin{array}{cc}1& 2\\ 4& 3\end{array}\right),B=\left(\begin{array}{cc}6& 8\\ 4& 2\end{array}\right)$

Tentukan penjumlahan dari matriks A dan matriks B

Jawab:

Contoh 2 :

Misalkan diberikan matriks sebagai berikut:

$S=\left[\begin{array}{cc}7& 5\\ 5& 3\\ 10& 4\end{array}\right],T=\left[\begin{array}{cc}4& 1\\ 1& 2\\ 5& 3\end{array}\right]$

Tentukan: S+T

Jawab:

$S+T=\left[\begin{array}{cc}7& 5\\ 5& 3\\ 10& 4\end{array}\right]+\left[\begin{array}{cc}4& 1\\ 1& 2\\ 5& 3\end{array}\right]$ $S+T=\left[\begin{array}{cc}11& 6\\ 6& 5\\ 15& 7\end{array}\right]$

Contoh 3 :

Diberikan matrik berordo 2x2, misalkan matriks P dan matriks Q sebagai berikut:

$P=\left[\begin{array}{cc}2& 3\\ 6& 9\end{array}\right],Q=\left[\begin{array}{cc}3& 1\\ 7& 5\end{array}\right]$

Tentukan: P - Q

Jawab:

Contoh 4 :

Misalkan diberikan matriks A berordo 3x3 dan B berordo 3x3 sebagai berikut:

$A=\left[\begin{array}{ccc}10& 28& 15\\ 16& 13& 13\\ 24& 27& 20\end{array}\right],B=\left[\begin{array}{ccc}9& 22& 10\\ 14& 10& 5\\ 20& 19& 8\end{array}\right]$

Tentukan: A - B 

Jawab:

             

            

Perkalian Matriks 

Matriks dapat dikalikan dengan sebuah bilangan bulat (skalar) atau dengan matriks yang lain. Masing- masing perkalian mempunyai syaratnya masing-masing.

Perkalian matriks ada dua, yaitu :

1. Perkalian skalar dengan matriks
    Suatu matriks yang dikalikan dengan bilangan bulat, maka hasilnya akan berupa matriks dengan elemen-elemen berupa hasil kali bilangan tersebut dengan elemen-elemen matriks sebelumnya.
Perkalian matriks dengan bilangan bulat dapat dikombinasikan dengan penjumlahan atau pengurangan asalkan dengan ordo yang sama. 
Sifat-sifat perkalian skalar dengan matriks
a. k(A+B) = kA + kB
b. k (A-B) = kA - kB

    
Contoh :

Diketahui konstanta k = 2 dan sebuah matriks A dengan persamaan seperti di bawah.

  

Maka hasil perkalian konstanta k dengan matriks A adalah sebagai berikut.

  

  

2. Perkalian matriks dengan matriks 

    Baris x Kolom

    Perkalian antara dua matriks, misalkan matriks A dan matriks B, dapat dilakukan jika jumlah kolom A sama dengan jumlah baris B. Perkalian ini akan menghasilkan matriks dengan jumlah baris sama dengan A dan jumlah kolom sama dengan B.

Perkalian matriks A yang berordo (mxn) dikali B yang berordo (nxm) akan menghasilkan C=AB yang berordo (mxm).

Perkalian matriks 2 x 2 secara umum

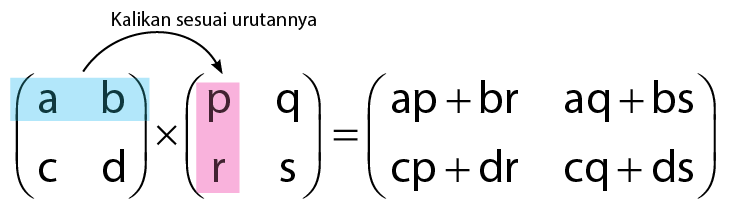
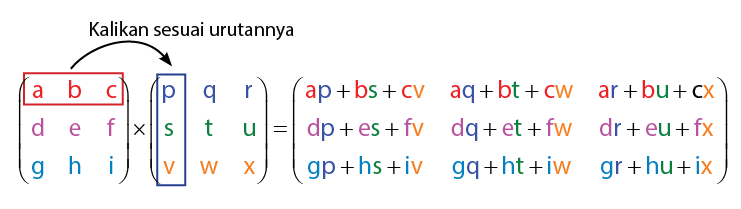
Perkalian matriks 3 x 3 secara umum

Contoh dua matriks yang tidak dapat dikalikan

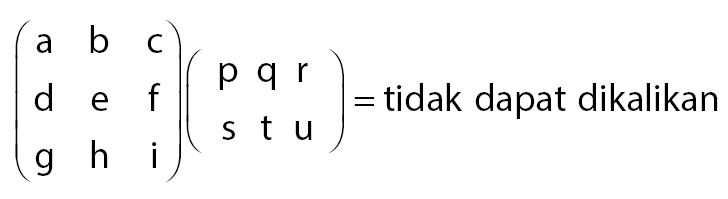
Matriks pertama mempunyai jumlah kolom sebanyak 3 dan matriks ke dua mempunyai jumlah baris sebanyak 2. Karena jumlah kolom pada matriks pertama tidak sama dengan jumlah baris pada kolom ke dua maka dua buah matriks tersebut tidak dapat dikalikan.

Sifat- sifat perkalian matriks

1. Asosiatif  (AB)C=A(BC)
2. Tidak komutatif 
3. Distribusi 

    Distribusi kiri A(B+C)= AB + AC

    Distribusi kanan (B + C) A = BA + CA

4. Asosiatif skalar (kA)B=A(kB)  

Contoh 1 :
Perkalian matriks 2 x 2
Tentukan hasil perkalian matriks A dan B di bawah!

  

  

Jawab:

  

  

  

  

Contoh 2 : perkalian matriks 3 x 3

Tentukan hasil perkalian matriks 3 x 3 di bawah!

  

  

Jawab:

  

  

  

  

Contoh 3 : perkalian matriks (3 x 3) x (3 x 2)

  

  

Jawab:

  

  

  

  

Demikian proses perkalian matriks 3 x 3 dengan 3 x 2, diperoleh matriks dengan ukuran 3 x 2

Contoh 4 :

Tentukan hasil kali dari matriks A dan B jika matriksnya sebagai berikut:$A=\left[\begin{array}{ccc}3& 5& 2\end{array}\right],B=\left[\begin{array}{c}3\\ 8\\ 1\end{array}\right]$

Jawab:

Baca juga Ringkasan Matriks- Pengertian, Jenis, Ordo, Transpose
https://idschool.net/sma/perkalian-matriks-3-x-3-2-x-2-dan-m-x-n-x-n-x-m/